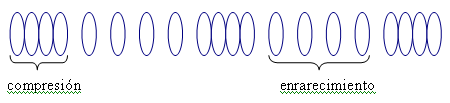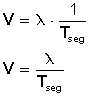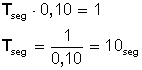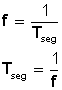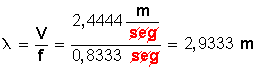MOVIMIENTO ONDULATORIO

Proceso por el que se propaga energía de un lugar a otro sin transferencia de materia, mediante ondas mecánicas o electromagnéticas. En cualquier punto de la trayectoria de propagación se produce un desplazamiento periódico, u oscilación, alrededor de una posición de equilibrio. Puede ser una oscilación de moléculas de aire, como en el caso del sonido que viaja por la atmósfera, de moléculas de agua (como en las olas que se forman en la superficie del mar) o de porciones de una cuerda o un resorte. En todos estos casos, las partículas oscilan en torno a su posición de equilibrio y sólo la energía avanza de forma continua. Estas ondas se denominan mecánicas porque la energía se transmite a través de un medio material, sin ningún movimiento global del propio medio. Las únicas ondas que no requieren un medio material para su propagación son las ondas electromagnéticas; en ese caso las oscilaciones corresponden a variaciones en la intensidad de campos magnéticos y eléctricos.

Oscilación

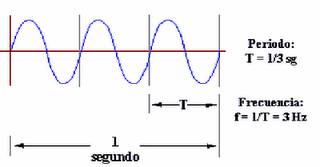
En física, química e ingeniería, movimiento repetido de un lado a otro en torno a una posición central, o posición de equilibrio. El recorrido que consiste en ir desde una posición extrema a la otra y volver a la primera,pasando dos veces por la posición central, se denomina ciclo. El número de ciclos por segundo, o hercios (Hz), se conoce como frecuencia de la oscilación.

Cuando se pone en movimiento un péndulo o se puntea la cuerda de una guitarra, el péndulo y la cuerda acaban deteniéndose si no actúan sobre ellos otras fuerzas. La fuerza que hace que dejen de oscilar se denomina amortiguadora. Con frecuencia, estas fuerzas son fuerzas de rozamiento, pero en un sistema oscilante pueden existir otras fuerzas amortiguadoras, por ejemplo eléctricas o magnéticas.

Flameo

Un tipo peligroso de vibración es la oscilación repentina y violenta conocida como flameo. Este fenómeno se produce sobre todo en las superficies de control de los aviones, pero también ocurre en los cables eléctricos cubiertos de escarcha cuando la velocidad del viento es elevada. Uno de los casos de flameo más espectaculares provocó en 1940 el hundimiento de un puente en Tacoma, Estados Unidos. La causa fue un viento huracanado cuya velocidad potenció la vibración del puente.

En el flameo, la amplitud de vibración de una estructura puede aumentar tan rápidamente como para que ésta se desintegre casi de forma instantánea. Por eso, impedir el flameo es muy importante a la hora de diseñar puentes y aviones. En el caso de los aviones, el análisis de flameo suele complementarse con pruebas realizadas con una maqueta del avión en un túnel aerodinámico.

Frecuencia

Término empleado en física para indicar el número de veces que se repite en un segundo cualquier fenómeno periódico. La frecuencia es muy importante en muchas áreas de la física, como la mecánica o el estudio de las ondas de sonido.

Las frecuencias de los objetos oscilantes abarcan una amplísima gama de valores. Los temblores de los terremotos pueden tener una frecuencia inferior a 1, mientras que las veloces oscilaciones electromagnéticas de los rayos gamma pueden tener frecuencias de 10²⁰ o más. En casi todas las formas de vibración mecánica existe una relación entre la frecuencia y las dimensiones físicas del objeto que vibra. Por ejemplo, el tiempo que necesita un péndulo para realizar una oscilación completa depende en parte de la longitud del péndulo; la frecuencia de vibración de la cuerda de un instrumento musical está determinada en parte por la longitud de la cuerda. En general, cuanto más corto es el objeto, mayor es la frecuencia de vibración.

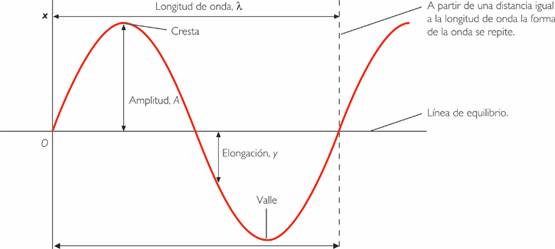
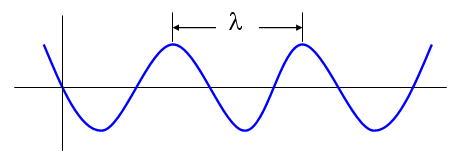
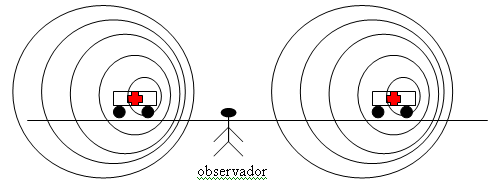
En todas las clases de movimiento ondulatorio, la frecuencia de la onda suele darse indicando el número de crestas de onda que pasan por un punto determinado cada segundo. La velocidad de la onda (v) y su frecuencia (f) y longitud de onda (L) están relacionadas entre sí. La longitud de onda (la distancia entre dos crestas consecutivas) es inversamente proporcional a la frecuencia y directamente proporcional a la velocidad.

v = l.f

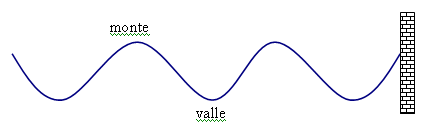
En una onda transversal, la longitud de onda es la distancia entre dos crestas o valles sucesivos. En una onda longitudinal, corresponde a la distancia entre dos compresiones o entre dos enrarecimientos sucesivos.

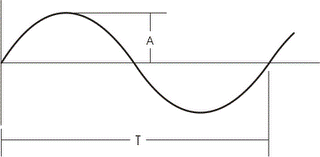
En el caso de una onda mecánica, su amplitud es el máximo desplazamiento de las partículas que vibran. En una onda electromagnética, su amplitud es la intensidad máxima del campo eléctrico o del campo magnético.

La frecuencia se expresa en hercios (Hz); una frecuencia de 1 Hz significa que existe 1 ciclo u oscilación por segundo. Las unidades como kilohercios (kHz) (miles de ciclos por segundo), megahercios (MHz) (millones de ciclos por segundo) y gigahercios (GHz) (miles de millones de ciclos por segundo) se usan para describir fenómenos de alta frecuencia como las ondas de radio. Estas ondas y otros tipos de radiación electromagnética pueden caracterizarse por sus longitudes de onda o por sus frecuencias.

Frecuencia natural

Cualquier objeto oscilante tiene una frecuencia natural, que es la frecuencia con la que tiende a vibrar si no se le perturba. Por ejemplo, la frecuencia natural de un péndulo de 1 m de longitud es de 0,5 Hz, lo que significa que el péndulo va y vuelve una vez cada 2 segundos. Si se le da un ligero impulso al péndulo cada 2 segundos, la amplitud de la oscilación aumenta gradualmente hasta hacerse muy grande. El fenómeno por el que una fuerza relativamente pequeña aplicada de forma repetida hace que la amplitud de un sistema oscilante se haga muy grande se denomina resonancia. Muchos problemas graves de vibración en ingeniería son debidos a la resonancia. Por ejemplo, si la frecuencia natural de la carrocería de un automóvil es la misma que el ritmo del motor cuando gira a una velocidad determinada, la carrocería puede empezar a vibrar o a dar fuertes sacudidas. Esta vibración puede evitarse al montar el motor sobre un material amortiguador, por ejemplo hule o goma, para aislarlo de la carrocería.

Tipos de ondas

Las ondas se clasifican según la dirección de los desplazamientos de las partículas en relación a la dirección del movimiento de la propia onda. Si la vibración es paralela a la dirección de propagación de la onda, la onda se denomina longitudinal. Una onda longitudinal siempre es mecánica y se debe a las sucesivas compresiones (estados de máxima densidad y presión) y enrarecimientos (estados de mínima densidad y presión) del medio. Las ondas sonoras son un ejemplo típico de esta forma de movimiento ondulatorio.

Otro tipo de onda es la onda transversal, en la que las vibraciones son perpendiculares a la dirección de propagación de la onda. Las ondas transversales pueden ser mecánicas, como las ondas que se propagan a lo largo de una cuerda tensa cuando se produce una perturbación en uno de sus extremos, o electromagnéticas,como la luz, los rayos X o las ondas de radio. En esos casos, las direcciones de los campos eléctrico y magnético son perpendiculares a la dirección de propagación. Algunos movimientos ondulatorios mecánicos, como las olas superficiales de los líquidos, son combinaciones de movimientos longitudinales y transversales, con lo que las partículas de líquido se mueven de forma circular.

Ondas Unidimensionales

Cuando una perturbación, en el estado físico de un sistema en un punto, se propaga conservando la forma de la perturbación, entonces, el proceso de propagación se llama onda. Si la forma de la perturbación se modifica a lo largo de la propagación, el proceso se llama difusión.

Los elementos básicos de la propagación ondulatoria son:

Se emite la perturbación en el estado del canal, se propaga transportando energía en forma de información.No se propaga materia.

Emisión	Propagación	Recepción
Antena F Fuente emisora. Introduce una perturbación en C (señal)	Canal C Medio transmisor. La perturbación se propaga a través de él. ONDAS TRANSVERSALES Cuando una cuerda tensa se pulsa o se roza la perturbación resultante se propaga a lo largo de ella. Dicha perturbación consiste en la variación de la forma de la cuerda a partir de su estado de equilibrio: los segmentos de la cuerda se mueven en una dirección perpendicular a la cuerda y por tanto perpendicularmente a la dirección de propagación de la perturbación. Una onda en la que la perturbación es perpendicular a la dirección de propagación se denomina onda transversal. Supón que produces una onda en una cuerda agitando el extremo libre hacia arriba y hacia abajo. En este caso el movimiento de la cuerda es perpendicular a la dirección del movimiento de la onda. Cuando el movimiento del medio (en este caso, la cuerda) es perpendicular a la dirección en que se propaga la onda, decimos que se trata de una onda transversal. Las ondas que se producen en las cuerdas tensas de los instrumentos musicales y en las superficies de los líquidos son transversales. También las ondas electromagnéticas que constituyen las ondas de radio y la luz son transversales. ONDAS LONGITUDINALES Las ondas en las que la perturbación es paralela a la dirección de propagación se denominan longitudinales. Un ejemplo muy importante lo constituyen las ondas sonoras propagándose en cualquier medio material (sólido, líquido o gaseoso). Durante la propagación de la onda, las moléculas del medio oscilan en la dirección de propagación.   No todas las ondas son transversales. En ciertos casos las partículas del medio se mueven de un lado a otro en la misma dirección en la que se propaga la onda. Las partículas se mueven a lo largo de la dirección de la onda en vez de hacerlo en sentido perpendicular. Una onda de este tipo es una onda longitudinal. Las ondas sonoras son ondas longitudinales Ondas y sonido Una onda es una perturbación que avanza o que se propaga en un medio material o incluso en el vacío. Cuando estas ondas necesitan de un medio material, se llaman ondas mecánicas. Las únicas ondas que pueden propagarse en el vacío son las ondas electromagnéticas. El sonido es un tipo de onda mecánica que se propaga únicamente en presencia de un medio material. Un cuerpo al vibrar imprime un movimiento de vaivén (oscilación) a las moléculas de aire que lo rodean, haciendo que la presión del aire se eleve y descienda alternativamente. Estos cambios de presión se trasmiten por colisión entre las moléculas de aire y la onda sonora es capaz de desplazarse hasta nuestros oídos. Las partes de la onda en que la presión aumenta (las moléculas se juntan) se llaman compresiones y aquellas en que la presión disminuye (las moléculas se alejan) se llaman enrarecimientos. Según la dirección de propagación, clasificamos las ondas en dos tipos: Ondas Longitudinales: Es cuando la vibración de la onda es paralela a la dirección de propagación de la propia onda. Estas ondas se deben a las sucesivas compresiones y enrarecimientos del medio, de este tipo son las ondas sonoras. Un resorte que se comprime y estira también da lugar a una onda longitudinal. El sonido se trasmite en el aire mediante ondas longitudinales. Otro ejemplo de onda longitudinal es aquella que se produce cuando se deja caer una piedra en un estanque de agua, Se origina una perturbación que se propaga en círculos concéntricos que, al cabo del tiempo, se extienden a todas las partes del estanque.  Ondas Transversales: Donde la vibración es perpendicular a la dirección de la onda. Las ondas transversales se caracterizan por tener montes y valles.Por ejemplo, las ondas que se forman sobre la superficie del agua al arrojar una piedra o como en el caso de una onda que se propaga  a lo largo de una cuerda tensa a la que se le sacude por uno de sus extremos. Características generales o elementos de las ondas Tren de ondas: Todas las ondas al moverse lo hacen una tras otra como si fuera un tren de donde se coloca un vagon tras otro. Nodo: Es el punto donde la onda cruza la línea de equilibrio. Elongación: Es la distancia entre cualquier punto de onda y su posición de equilibrio. Cresta, monte o pico: es el punto más alto de una onda Valle: Es el punto más bajo de una onda. Periodo: Tiempo que tarda en efectuarse una onda o vibracion completa, se mide en segundos o s/ciclo se representa con una T mayúscula. Notemos que el periodo (T) es igual al recíproco de la frecuencia (f) y viceversa. Amplitud (A) : Es la maxima separacion de la onda o vibración desde su punto de equilibrio. La longitud de onda (λ) es la distancia entre dos máximos o compresiones consecutivos de la onda. En las ondas transversales la longitud de onda corresponde a la distancia entre dos montes o valles, y en las ondas longitudinales a la distancia entre dos compresiones contiguas. También podemos decir que es la distancia que ocupa una onda completa, se indica con la letra griega lambda (Λ) y se mide en metros. A la parte superior de la onda se le llama cresta y a la inferior se le llama valle. Tomaremos como ejemplo ilustrativo una onda transversal. Frecuencia: Es el número de ondas producidas por segundo. La frecuencia se indica con la letra f minúscula. Se mide en ciclos/ segundo o hertz (Hz). Coincide con el número de oscilaciones por segundo que realiza un punto al ser alcanzado por las ondas. Las dos magnitudes anteriores, longitud y frecuencia, se relacionan entre sí para calcular la velocidad de propagación de una onda. Velocidad de propagación: Es la relación que existe entre un espacio recorrido igual a una longitud de onda y el tiempo empleado en recorrerlo. Se indica con la letra V y es igual al producto de la frecuencia (f) por la longitud de onda (λ). Matemáticamente se expresa así:  por lo tanto fórmula que nos indica que la longitud de onda λ y la frecuencia f son dos magnitudes inversamente proporcionales, es decir que cuanto mayor es una tanto menor es la otra. Periodo: Es el tiempo (en segundos) que tarda un punto en realizar una oscilación completa al paso de una onda. Se abrevia con la letra (T). La frecuencia (f) se relaciona con el periodo según la fórmula Volvamos a la fórmula  para reemplazar en ella f (frecuencia), y nos queda la fórmula Lo cual nos indica que también podemos calcular la velocidad si conocemos la longitud  (λ) y el periodo (en segundos) de una onda. Como vemos, podemos relacionar estas magnitudes  y conociendo los valores de algunas de ellas podemos determinar los valores de las otras, usando las fórmulas indicadas. Para ejercitar la materia desarrollemos algunos problemas Problema 1 El edificio Platinum, ubicado en Santiago, se mece con una frecuencia aproximada a 0,10 Hz. ¿Cuál es el periodo de la vibración? Datos: Frecuencia  f = 0,10 Hz Fórmula: Reemplazamos los valores Calculamos Tseg Respuesta: El periodo (intervalo de duración entre dos crestas de una onda) es de 10 segundos. Problema 2 Una ola en el océano tiene una longitud de 10 m. Una onda pasa por una determinada posición fija cada 2 s. ¿Cuál es la velocidad de la onda? Datos: Longitud  (λ) = 10 m Periodo (Tseg) = 2 seg Velocidad (V) =  ¿ Fórmula: Reemplazamos valores Respuesta: La velocidad de una onda de 10 metros que pasa por una posición fija cada 2 segundos es de 5 m/s Problema 3 Ondas de agua en un plato poco profundo tienen 6 cm de longitud. En un punto, las ondas oscilan hacia arriba y hacia abajo a una razón de 4,8 oscilaciones por segundo. a) ¿Cuál es la rapidez de las ondas?, b) ¿cuál es el periodo de las ondas? Datos: longitud (λ) = 6 cm frecuencia (f) = 4,8 Hz Fórmula: Periodo (T) = ¿ Velocidad (V) = ¿ Para calcular la velocidad (V) necesitamos conocer la longitud (6 cm) y el periodo (T), ya que la fórmula de V es y la fórmula para determinar el periodo (T) la obtenemos de reemplazamos valores y queda entonces quedará Respuestas La rapidez o velocidad de las ondas es de 28,8 cm/s;  y el periodo de cada onda es de 0,2083333 seg. Problema 4 Ondas de agua en un lago viajan 4,4 m en 1,8 s. El periodo de oscilación es de 1,2 s. a) ¿Cuál es la rapidez de las ondas?, b) ¿cuál es la longitud de onda de las ondas? Datos: Distancia recorrida por las ondas: 4,4 m Tiempo en recorrer esa distancia: 1,8 seg Periodo: 12,2 seg Primero calculamos la velocidad Ahora, calculamos la frecuencia (f) Luego, calculamos la longitud de onda (l) Respuestas La rapidez o velocidad de las ondas es de 2,4444 m/s;  y la longitud de cada onda es de 2,9333 m Problema 5 Calcular la longitud de onda de una nota musical con una frecuencia de 261 Hz. Considerando que la velocidad de propagación del sonido en el aire a 15° C es de 340 m/seg, entonces se tiene, v = 340 m/seg ;           f =261 Hz ;      por lo tanto la longitud de onda es, El efecto Doppler Cuando una fuente de sonido se acerca o aleja de un observador, el tono del sonido percibido varía. Este fenómeno se conoce como efecto Doppler y fue explicado por primera vez en 1842 por el físico austriaco Christian Doppler (1803-1853). Tomemos por ejemplo la sirena de una ambulancia. Cuando se acerca, las ondas sonoras que se propagan hacia delante están más apretadas, y llegan a nuestros oídos con más frecuencia y la sirena tiene un tono más agudo. Cuando se aleja, las ondas que se propagan hacia atrás están mas separadas, de frecuencia más baja y el sonido es más grave. Cuanto mayor es la velocidad de la fuente de sonido mayor es el cambio de frecuencia. Ondas estacionarias Cuando dos ondas de igual amplitud, longitud de onda y velocidad avanzan en sentido opuesto a través de un medio se forman ondas estacionarias. Por ejemplo, si se ata a una pared el extremo de una cuerda y se agita el otro extremo hacia arriba y hacia abajo, las ondas se reflejan en la pared y vuelven en sentido opuesto. Esta onda tiene la misma frecuencia y longitud de onda que la onda original. Con determinada frecuencias las dos ondas, propagándose en sentidos contrarios interfieren para producir una onda estacionaria. Estas ondas están caracterizadas por la aparición de puntos en reposo (nodos) y puntos con amplitud vibratoria máxima (vientre). Esto es posible observarlo en las cuerdas vibrantes, como en las cuerdas de guitarra, y en los tubos sonoros. Las ondas estacionarias no son ondas viajeras sino los distintos modos de vibración de una cuerda, una membrana, aire en un tubo, etc. Cuerdas vibrantes Una cuerda, tendida entre dos puntos fijos, es susceptible de emitir un sonido gracias a sus vibraciones. La nota producida por una cuerda vendrá determinada por la longitud (L), la tensión (T), la densidad (d) y la sección (S). Así, si disponemos de una cuerda muy tensa y fina, obtendremos una nota aguda; y por el contrario, si la cuerda está poco tensa y es gruesa, la nota será grave. La frecuencia se puede encontrar a partir de la fórmula:  Resonancia La frecuencia a la que un objeto vibra de manera natural se llama su frecuencia de resonancia, si un sonido que posea esa frecuencia se emite en las proximidades de un objeto, este capta la energía de la onda sonora y vibra de manera natural produciéndose la resonancia. Cuando la música suena alta en una habitación, determinadas notas harán que resuene un objeto situado cerca de los parlantes. Una copa de cristal se puede romper si un cantante es capaz de emitir un sonido de frecuencia igual a la frecuencia natural de la copa. En resumen, un cuerpo vibra por resonancia cuando llegan a él vibraciones de frecuencia igual a la propia vibración del cuerpo. Espectro sonoro, Infrasonido y Ultrasonido No todas las ondas sonoras pueden ser percibidas por el oído humano, el cual es sensible únicamente a aquellas cuya frecuencia están comprendida entre los 20 y los 20.000 Hz, pudiendo variar de una persona a otra. A las perturbaciones de frecuencia inferior a los 20 Hz se les denomina infrasonidos y  a las que la tienen rango superior a 20.000 Hz, ultrasonido. Tanto el infrasonido como el ultrasonido no son perceptibles por el oído humano. El infrasonido es el tipo de onda generada por grandes fuentes sonoras, como es el caso de los terremotos y volcanes, así como por maquinarias muy pesadas. Se ha comprobado que este tipo de onda puede provocar movimiento e irritación de los órganos internos del cuerpo. El ultrasonido tiene muchas aplicaciones en diferentes campos de la física, la química, la tecnología y la medicina. Se utiliza a menudo en medicina porque, a diferencia de los rayos X, las ondas ultrasónicas no perjudican a los tejidos humanos. La ecografía se basa en la emisión de dichas ondas a través de la piel hacia los órganos en exploración, estos las reflejan y los ecos son recogidos por un escáner que forma en ellos una imagen sobre una pantalla. El ultrasonido también es utilizado en la medición de profundidades marítimas, para localizar cardúmenes, con lo que resulta una excelente ayuda para la pesca, así como para detectar barcos hundidos y submarinos. Se le utiliza además en la industria para le detección de grietas en los metales, por medio de la diferencia en los ecos reflejados en la grieta. Otro tipo de aplicación de las ondas ultrasonoras es la de matar microorganismos; al enfocar sobre ellos un haz ultrasónico, los hace entrar en rapidísima vibración, con lo cual mueren. Existen animales capaces de emitir ondas ultrasonoras: Los delfines, por medio de fuertes chasquidos que rebotan en los objetos produciendo ecos, pueden localizar peces y otros objetos submarinos. Los murciélagos son capaces de viajar y detectar obstáculos por medio de las ondas ultrasónicas que son capaces de emitir y percibir.	Receptor La perturbación recibida es absorbida

Procesos Termodinámicos.

*PROCESOS TERMODINÁMICOS*

 

La información que les ofrezco es un breve resumen de los “Procesos Termodinámicos”. Al igual que se complementa con ejemplos y algunos ejercicios para reforzar nuestros conocimientos para que se entienda de una manera mas sencilla.

 PROCESOS TERMODINÁMICOS

Los procesos termodinámicos comprenden el comportamiento y relación que se da entre las temperaturas, presión y el volumen es importante en diversos procesos industriales. 

2.1.1 TERMODINÁMICA:
También es conocida como el movimiento del calor, en esta rama de la física se estudia la transferencia de calor en trabajo mecánico y viceversa. su principal base es la conservación de la energía.
Nos proporciona una teoría básica que nos sirve para entender y poder diseñar maquinas térmicas (refrigeradores, cohetes, etc.).

SISTEMA TERMODINAMICO:Es una parte del universo que se separa con la finalidad poderla estudiar. Para ello se aísla de los alrededores a través de límites o fronteras, de tal manera que todo lo que se encuentra fuera de lo delimitado se denomina alrededores.

a) Frontera:Es el limite que separa al sistema de lo alrededores, casi siempre son paredes que pueden ser diatérmicas o adiabáticas.

b) Pared diatérmicas:Es una conductora de calor, ésta permite el intercambio de calor entre el sistema y sus alrededores y al revés.

c) Pared adiabática:Es caracterizada por NO permitir la interacción térmica del sistema con los alrededores. Es construida de materiales no conductores del calor como porcelana o asbesto.

d) Equilibrio termodinámico:Se alcanza cuando después de cierto tiempo de poner en contacto un sistema de baja temperatura con otro sistema a mayor temperatura se iguala, por lo tanto existe un intercambio de calor, las propiedades de presión, densidad y temperatura cuando se encuentran en este punto dejan de variar.

e) Energía interna ( Ei):Es la energía contenida en el interior de las sustancias. Es la suma de energía cinética y potencial de las moléculas individuales que la forman. La mayoría de las veces se cumple cuanto mayor sea la temperatura de un sistema también lo será su energía interna.
La energía interna se hace presente en las sustancias combustibles y es proporcional a la masa.

2.1.2 EQUIVALENTE MECANICO DEL CALOR:

Fue establecido por un físico ingles llamado James Prescott Joule (1818-1889), es autor de importantes trabajos sobre la TEORIA MECANICA DEL CALOR, a mediados del sigo XIX. Demostró que cierta variación de temperatura indica un cambio de energía interna y aparece que se pierde determinada cantidad de energía molecular.
Después de varios experimentos en los cuales todos los resultados le daban 1J = 0.24 cal o 1 cal = 4.2J, concluyo que la energía mecánica y la energía que causaba la diferencia de temperatura eran equivalentes.

2.1.2 PRIMERA LEY DE LA TERMODINAMICA.
Esta ley dice que la variación de la energía interna de un sistema es igual a la energía que transfieren o reciben los alrededores en forma de calor y trabajo, de forma tal que se cumple la energía no se crea ni se destruye, solo se transforma.
La primera ley de la termodinámica se muestra matemáticamente de la siguiente manera:

a) Peso termodinámico:Es cuando la temperatura, presión o volumen de un gas varían. Los procesos termodinámicos se clasifican en:

2.1.2 PROCESO ISOTERMICO:
Se presenta cuando la temperatura del sistema, permanece constante independientemente de los cambio de presión o volumen que sufran.

Este proceso se rige por la ley de Boyle-Mariotte de Robert Boyle (1626-1691), Físico Químico irlandés conocido por sus experimentos acerca de las propiedades de los gases
y Edme Mariotte (1620-1684), Físico Francés que descubrió la ley que relación la presión y el volumen de los gases a temperatura constante.

Si un proceso isotérmico formado por un gas experimenta una expansión isotérmica, para que la temperatura permanezca constante la cantidad de calor recibido debe ser igual al trabajo que realiza durante la expansión. Pero si presenta una compresión isotérmica, para que la temperatura también permanezca constante el gas tiene que liberar una cantidad de calor igual al trabajo desarrollado sobre él.
La temperatura no cambia, su energía interna (Ei), son constantes y su variación de energía interna (ΔEi) es igual a cero, por lo que se cumple que (Ei es constante) (ΔEi = 0 ) Q=Tr.

2.1.2 PROCESO ISOBARICO:
Es cuando hay una variación del volumen o temperatura y la presión permanece constante, no importando si el gas sufre una compresión o una expansión. Este proceso rige por la Ley de Charles: Jackes A. Charles ( 1742-1822). Químico, físico y aeronauta Frances, que fue el primero en hacer mediciones acerca de los gases que se expanden al aumentar la temperatura.
Las ecuaciones para el proceso isobárico son:

2.1.2 PROCESO ISOCORICO:Se presenta cuando el volumen del sistema permanece constante. Ya que la variación del volumen es cero, no se realiza trabajo sobre el sistema ni de éste último de sobre los alrededores, por lo que se cumple Tr = 0 Y ΔEi = Q, esto indica que todo el calor suministrado aumentara en la misma proporción a la energía interna, en general esto se presenta cuando un gas se calienta dentro de un recipiente con volumen fijo.
Cuando se calientan dos masas iguales de gas, a una presión constante y otra a volumen constante, para que logren el mismo incremento de temperatura se requiere proporcionar mayor calor al sistema a presión constante (Qp>Qv). Ello se debe a que en el proceso isobárico el calor suministrado se usa para aumentar la energía interna y efectuar trabajo, mientras que en el proceso isocórico todo el calor se usa para incrementar exclusivamente la energía interna.

2.1.3 PROCESO ADIABATICO:
Ocurre cuando el sistema no crea ni recibe calor, cumpliéndose que (Q=0) y ΔEi = -Tr , aun cuando el gas puede presentar expansión o comprensión.
En resumen las condiciones que se tienen que cumplir para los procesos son termodinámicos son:

CALENTAMIENTO POR COMPRESION:
Si un gas sufre compresión rápida, disminuye su volumen, se produce calor y se incrementa la temperatura.

EJEMPLOS

ISOBARICO:Un dispositivo cilindro émbolo contiene un gas que está inicialmente a 1 Mpa y ocupa 0.020 m3. El gas se expande hasta un volumen final de 0.040 m3. Determine el trabajo obtenido en Kj para un proceso isobárico (a presión constante).

Para calcular el trabajo en procesos a presión constante se utiliza la Ec.
W1-2 = P (V2 – V1) =
Se tienen los volúmenes en metros cúbicos y la presión en unidades de mega pascales, hay que utilizar unidades homogéneas: Conociendo que un Kpa = Kj/ m3, se puede convertir la presión de Mpa a Kpa.
1 Mpa * 1000 Kpa = 1000 Kpa. 1 Mpa
Se sustituye en la Ec.4: W1-2 = P (V2 – V1) = 1000 Kj/ m3 *(0.040 m3 – 0.020 Kj/ m3)
W1-2 = 20Kj

Un gas ideal en el que C v = 5.n.R/2 es trasladado del punto "a" al punto "b" Siguiendo los caminos acb, adb y ab, la presión y el volumen finales son P 2 = 2P 1 y V 2 = 2V 1 . a) Calcular el calor suministrado al gas, en función de n, R y T 1 en cada proceso. b) Cual es la capacidad calorífica en función de R para el proceso ab.

Aplicando el primer principio de la termodinámica podemos escribir:

Para cualquiera de los procesos que hemos de considerar, la variación de energía interna será el mismo puesto que U es una función de estado y solo depende de los puntos inicial y final del proceso. Por tratarse de un gas perfecto, podemos escribir :

Pero, de la ecuación de los gases perfectos, obtenemos :

por lo que, sustituyendo

Calculamos el trabajo en cada uno de los procesos :

En el caso de W ab no conocemos el tipo de proceso que sigue el gas, pero podemos ver que el trabajo vendrá dado por :


Obtenidos todos los datos necesarios podemos calcular el calor suministrado al gas en cada uno de los procesos :

Finalmente, la capacidad calorífica para el proceso ab será, en realidad, la capacidad calorífica media que podemos calcular mediante:

Un sistema cerrado, inicialmente en reposo sobre la tierra, es sometido a un proceso en el que recibe una transferencia neta de energía por trabajo igual a 200KJ. Durante este proceso hay una transferencia neta de energía por calor desde el sistema al entorno de 30KJ. Al final del proceso el sistema tiene una velocidad de 60m/s y una altura de 60m. La masa del sistema es 25Kg, y la aceleración local de la gravedad es g=9,8m/s2. Determinar el cambio de energía interna del sistema para el proceso.

ACTIVIDADES DE APRENDIZAJE

1.- Si en un sistema el gas sufre una expansión adiabática. ¿Cuánto calor es trasferido a los alrededores?

a) Cero

b) Muy poco

c) Regular

d) Demasiado

2.- Si la variación de la energía interna es cero, el proceso que efectúa el sistema es…

a) adiabático

b)isobárico

c)isocórico

d) isotérmico

3.- Si un sistema absorbe calor y realiza trabajo debido a su expansión, de forma tal que su variación de energía interna es negativa, ello indica que el trabajo es:

a) mayor que el calor absorbido

b) menor que el calor absorbido

c) cero respecto al calor absorbido

d) constante respecto al calor absorbido

4.- Un gas contenido en un cilindro con pistón se expande al ponerlo en contacto con calor. Si la energía interna no varia, el trabajo realizado por el gas es __________ al calor absorbido.

a) Cero

b) igual

c)mayor

d)menor

5.- Si el sistema de un gas realiza trabajo disminuye su ______ y el signo asociado es ______
a)calor - negativo

b)calor - constante

c)energía interna - positivo

d) energía interna – negativo

6.- En un proceso termodinámico en el que el volumen es constante, ¿Qué condición se cumple?
a)Tr=Q y ΔEi=0

b)Tr=0 y ΔEi=0

c)Tr=0 y ΔEi=Q

d) Tr=Q y ΔEi=Q

7.- Considerando que el sistema sea diatérmico, si este absorbe calor, su energía interna _______ y el signo del calor es _________
a) disminuye - negativo

b)aumenta – positivo

c)es constante - positivo

d)aumenta - negativo

8.- Si el sistema libera calor, disminuye su ______ y el signo del calor será _________
a) energía interna - negativo

b) temperatura - positivo

c)temperatura - constante

d)energía interna - cero

9.- El proceso en el cual todo el trabajo suministrado al sistema incrementa en la misma proporción la energía interna se llama....a) isocórico

b)isobárico

c)adiabático

d)isotérmico

10.- Nombre del proceso en el que no se efectúa trabajo mecánico, ya que no hay variación de volumen:a) isobárico

b)isocórico

c)isotérmico

d)adiabático

11.- Nombre del proceso en el que varían el volumen y la temperatura, por lo que el sistema puede hacer o recibir trabajo mecánico:
a)adiabático

b)isobárico

c)isocórico

d)isotérmico

12.- Nombre del proceso donde no existe intercambio de calor con los alrededores.
a)isotérmico:

b)adiabático

c)isocórico

d)isobárico

13.- Una expansión rápida de un gas ocasiona…..
a) disminución de temperatura y de energía interna.

b) aumento de temperatura y disminución de presión.

c) aumento de volumen y presión.

d) diminución de temperatura y aumento de energía interna.

• Relaciona las dos columnas colocando en el paréntesis de la izquierda la letra que corresponda. Cada letra puede usarse solo una vez.

A - Expansión de un gas

B - Proceso isobárico

C - Proceso isotérmico

D - Compresión de un gas

E - Proceso adiabático

F - Proceso isocórico

14.- ( E ) No hay intercambio de calor con los alrededores
15.- ( A ) La temperatura disminuye

16.- ( F ) No se efectúa trabajo mecánico
17.- ( B ) La presión permanece constante
18.- ( D ) La temperatura aumenta

• Coloca en el paréntesis una V si la aseveración es correcta y una F si es falsa.
  con respecto a procesos termodinámicos:

19.- ( V ) En una expansión adiabática la energía interna del sistema disminuye.
20.- ( V ) En una compresión adiabática la temperatura del sistema permanece constante.
21.- ( V ) En un proceso isotérmico el calor absorbido por el sistema gaseoso es igual al trabajo que el realiza sobre los alrededores.
22.- ( V ) En un proceso isotérmico se realiza trabajo.
23.- ( F ) En una expansión adiabática el sistema gaseoso absorbe calor.

• Coloca sobre la línea una o dos palabras que completen el enunciado:

24.- La termodinámica es la rama de la física que se encarga de estudiar la transformación del calor en trabajo mecánico.
25.- Las paredes diatérmicas permiten el intercambio de calor entre el sistema y los alrededores
26.- La energía interna es la suma de energía cinética y potencial que poseen las moléculas de las sustancias
27.- En un proceso isotérmico la energía interna permanece constante debido a que la temperatura no varia.
28.- La primera ley de la termodinámica establece que la variación de energía interna en un sistema es igual a la energía que transfieren o reciben los alrededores en forma de calor y trabajo.
29.- Si un gas esta encerrado en un cilindro con pareces aislantes y puede comprimirse o expandirse, en este sistema no podrá ceder ni tampoco recibircalor.
30.- En un proceso adiabático el calor intercambiado tiene un valor de cero.
31.- El trabajo tiene signo positivo cuando el sistema recibe trabajo de los alrededores.
32.- Si el sistema recibe calor del exterior se le asocia el signo positivo.
33.- Si la variación de la energía interna es igual al trabajo desarrollado se trata de un proceso adiabático.

• Coloca en el paréntesis una V si la aservacion es correcta y una F si esta es falsa.
  En un proceso isotermico:

34.- ( F ) El calor puede aparecer en forma de aumento de energía interna.
35.- ( F ) El gas puede ceder calor realizado trabajo sobre los alrededores.
36.- ( V ) Todo el calor se transforma en trabajo mecanico.
37.- ( V ) Si sufre una expansión, puede introducirse en un calentador para que no se altere la temperatura.
38.- ( F ) Cualquier punto de la isotermia tiene diferente temperatura.

• Relaciona las columnas colocando en el paréntesis de la izquierda la letra que corresponda. Cada letra puede usarse solo una vez.

A - Sistema en trabajo mecánico

B - Equilibrio termodinámico.

C - Termodinámica.

D - Energía interna y alrededores

E - Equivalente mecánico del calor

F - Pared diatérmica de las partículas de las sustancias.

39.- ( C ) Estudia la transformación de calor
40.- ( A ) Frontera y alrededores son parte de…
41.- ( F ) Permite el intercambio de calor entre sistema
42.- ( B ) Los cuerpos se encuentran a la misma temperatura.
43.- ( D ) Representa la suma de la energía cinética y potencial.

• Coloca en el paréntesis una V si la aceración es correcta y una F si esta es falsa.
  En un proceso adiabático

44.- ( V ) el sistema puede sufrir una expansión o una compresión.
45.- ( F ) Si se comprime su temperatura aumenta.
46.- ( F ) Hay una transferencia de calor.
47.- ( F ) Todo el trabajo realizado por los alrededores incrementa la energía interna.
48.- ( V ) Un ejemplo de este proceso es guardar una sustancia en un termo.

• A continuación se presentan problemas en los que se aplican las ecuaciones de la primera ley de la termodinámica y de los procesos termodinámicos. Para que estés seguro de que el procedimiento fue el adecuado, se muestran los resultados.

1.- Cierto gas contenido en un cilindro con embolo absorbe 50 calorías, por lo que realiza un trabajo mecánico de 300J. ¿Cuál fue la variación de la energía interna?
Datos:

Q=50cal
Tr=300J

Calcular:Variacion de la energía interna

Formula:ΔEi=Q-Tr
1cal=4.2J

Sustitucion y operación:
ΔEi = 210J – 300J = -90J

2.- Un gas contenido en un cilindro con embolo, al aplicarle un trabajo de 180J hace que la variación de energía interna adquiera un valor de 75J. ¿Qué cantidad de calor es cedido a los alrededores?
Datos:

Tr=180J
ΔEi = 75J

Calcular:
Calor cedido a los alrededores

Formula:ΔEi=Q-Tr
Q = ΔEi - Tr

Sustitución y operación:
Q = 75J – 180J = -105J

3.- Sobre un sistema gaseoso se efectúa un trabajo de 120J y , como consecuencia, se liberan 41 calorías. ¿Qué variación de energía interna tiene?
Datos:

Tr=120J
Q=41cal

Calcular:Variación de la anergia interna

Formula:
ΔEi=Q-Tr
1cal = 4.2J

Sustitución y operación:
Tr = 120 J (dentro = - )
Q = 172.2J (se liberan = - )
ΔEi = -172.2J – (-120J) = -52.2